Chương 3: KÉO (NÉN) ĐÚNG TÂM

2.1. Định nghĩa – Nội lực

2.1.1. Định nghĩa

Thanh được gọi là kéo hoặc nén đúng tâm khi trên mọi mặt cắt ngang của thanh chỉ có một thành phần nội lực là lực dọc trục N_z. Ta gặp trường hợp này khi thanh chịu tác dụng của lực ở hai đầu thanh, dọc trục thanh lực có hai trị số bằng nhau và trái chiều.

Thực tế ta có thể gặp các cấu kiện chịu kéo hay nén đúng tâm như:

3.1.2. Nội lực

Để xác định và vẽ biểu đồ nội lực người ta dùng phương pháp mặt cắt, cắt qua các vị trí cần xác định nội lực, xét sự cân bằng một phần thanh, sử dụng phương trình cân bằng xác định lực dọc trên đạn thanh cần xác định:

      

3.2. Ứng suất pháp trên mặt cắt ngang

3.2.1. Thí nghiệm

Xét thanh chịu kéo đúng tâm, trên mặt thanh vạch các hệ thống lưới như hình vẽ:

- Hệ những đường thẳng song song với trục thanh được gọi là thớ dọc.

- Hệ những đường thẳng vuông góc với trục thanh tương ứng với các mặt cắt ngang.

3.2.2. Quan sát thí nghiệm

Khi thanh chịu kéo, ta quan sát thấy:

- Những đường thẳng song song với trục của thanh vẫn song song với trục của thanh và khoảng cách hai đường kề nhau dường như không thay đổi.

- Những đường thẳng vuông góc với trục của thanh vẫn vuông góc với trục của thanh và khoảng cách giữa chúng có sự thay đổi.

3.2.3. Các giả thiết về biến dạng

- Giả thiết 1: Giả thiết mặt cắt ngang phẳng (Bernoulli)

Mặt cắt ngang trước biến dạng là phẳng và vuông góc với trục thanh thì sau biến dạng vẫn phẳng và vuông góc với trục thanh.

- Giả thiết 2: Giả thiết về các thớ dọc

       Các lớp vật liệu dọc trục không có tác dụng tương hỗ lẫn nhau (không chèn, ép, xô, đẩy lẫn nhau) nên ta được σ_x = σ_y = 0.
       Ứng xử của vật liệu tuân theo định luật Hooke nghĩa là ứng suất tỉ lệ thuận với biến dạng.

3.2.3. Các giả thiết về biến dạng

Từ giả thiết 1: Mặt cắt ngang trước biến dạng là phẳng và vuông góc với trục thanh thì sau biến dạng vẫn phẳng và vuông góc với trục thanh, ta được τ = 0.

Từ giả thiết 2: Các lớp vật liệu dọc trục không có tác dụng tương hỗ lẫn nhau (không chèn, ép, xô, đẩy lẫn nhau), ta được σ_x = σ_y = 0.

Do đó, trên mặt cắt ngang chỉ tồn tãi duy nhất thành phần ứng suất pháp σ_z. Theo định nghĩa lực dọc trên mặt cắt ngang:

Theo định luật Hooke ta có: 

                                  

         



3.3. Biến dạng - Hệ số Poisson

3.3.1. Biến dạng dọc

Thanh có chiều dài L chịu tác dụng của lực kéo hoạc nén dọc trục sẽ bị biến dạng một đoạn ΔL.

3.3.2. Hệ số Poisson

Theo phương dọc thanh chịu kéo hoặc nén đúng tâm có biến dạng dọc trục tương đối (theo phương trục thanh z) là ε_z.

Theo phương ngang thanh (theo phương x, y) cũng có biến dạng được gọi là biến dạng ngang.  Nếu gọi biến dạng ngang tương đối theo hai phương x, y là ε_x, ε_y, Poisson đã tìm ra mối liên hệ sau:

3.4. Đặc trưng cơ học của vật liệu

3.4.1. Khái niệm

Đặc trưng cơ học của vật liệu là thông số đánh giá khả năng chịu lực, chịu biến dạng của vật liệu trong từng trường hợp chịu lực cụ thể.

Để xác định đặc trưng cơ học của vật liệu người ta tiến hành các thí nghiệm với các loại vật liệu khác nhau.

3.4.2. Phân loại

Căn cứ vào biến dạng và sự phá hỏng, khả năng chịu kéo, nén khác nhau người ta phân vật liệu thành hai loại cơ bản là vật liệu dẻo và vật liệu giòn:

       - Vật liệu dẻo là vật liệu bị phá hoại khi biến dạng lớn.

       - Vật liệu giòn là vật liệu bị phá hỏng khi biến dạng nhỏ.

  Dựa vào đặc điểm phá hủy, người ta chia thành: Rất dẻo, dẻo vừa và giòn.

Dựa vào đặc điểm biến dạng, người ta chia thành: Biến dạng lớn, trung bình và nhỏ.

Dựa vào dự báo biến dạng, ta có: phá hủy luôn báo trước, phá hủy báo trước và phá hủy không báo trước.

3.4.3. Thí nghiệm

a. Mục tiêu thí nghiệm

Xác định khả năng chịu lực của vật liệu.

Xác định khả năng chịu biến dạng.

Xác định các tính chất của vật liệu như:

       - Đặc trưng cơ học của vật liệu như giới hạn tỉ lệ, giới hạn chảy, giới hạn bền.

       - Độ cứng, độ mềm.

       - Độ bền uốn, độ bền phá hủy,...

       - Nhiệt độ, độ ẩm, …

Xác định đồ thị ứng suất biến dạng của vật liệu: không phụ thuộc vào kích thước tiết diện của mẫu thử từ đó xác định cơ tính của vật liệu.

b. Các phương pháp  thí nghiệm

Hai phương pháp được sử dụng để xác định phân loại của vật liệu đó là kéo và nén.

Trong các thí nghiệm này, mẫu thí nghiệm có hình dạng, kích thước theo qui định của các tiêu chuẩn tương ứng (TCVN, ISO, ASTM, …)

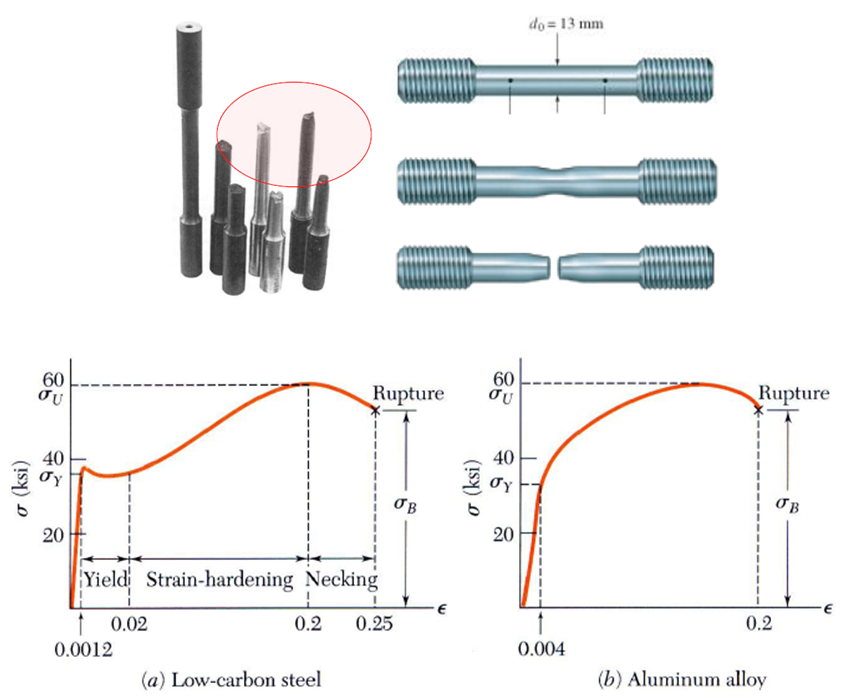
c. Thí nghiệm kéo mẫu vật liệu dẻo

       Mẫu thí nghiệm có chiều dài L₀ và đường kính d₀, diện tích A₀ theo tiêu chuẩn TCVN 197-85.

Tăng lực kéo từ 0 đến khi mẫu đứt, với bộ phận vẽ biểu đồ của thiết bị thí nghiệm, ta nhận được đồ thị quan hệ giữa lực kéo P và biến dạng dài ΔL của mẫu. Từ đó suy ra mối quan hệ giữa ứng suất pháp σ và biến dạng ε của vật liệu làm thí nghiệm.

       Đồ thị tương quan giữa ứng suất - biến dạng của thí nghiệm kéo mẫu vật liệu dẻo:

c. Thí nghiệm nén mẫu vật liệu dẻo

        Tương tự như kéo vật liệu dẻo, nén vật liệu dẻo cũng có biểu đồ quan hệ ứng suất biến dạng như sau:

Nhận xét: Đối với vật liệu dẻo thì giới hạn bền và giới hạn chảy của vật liệu khi nén và khi kéo bằng nhau hay khả năng chịu kéo và khả năng chịu nén của vật liệu dẻo là như nhau.

d. Thí nghiệm kéo mẫu vật liệu giòn

Thí nghiệm tương tự như trong thí nghiệm kéo vật liệu dẻo, đối với vật liệu giòn ta không thể xác định được giới hạn tỉ lệ, giới hạn chảy mà ta chỉ xác định được giới hạn bền.

Quan hệ giữa ứng suất – biến dạng của vật liệu giòn khi kéo có biểu đồ như hình vẽ:

e. Thí nghiệm nén mẫu vật liệu giòn

       Thí nghiệm tương tự như trong thí nghiệm kéo vật liệu giòn, khi kéo vật liệu giòn quan hệ giữa ứng suất – biến dạng của vật liệu giòn khi kéo có biểu đồ như hình vẽ:

3.5. Thế năng biến dạng đàn hồi

3.5.1. Định nghĩa

Theo định luật bảo toàn thì: công của ngoại lực A = thế năng tích lũy trong thanh. Thế năng tích lũy trong thanh được gọi là thế năng biến dạng đàn hồi, ký hiệu là U.

Do đó ta có:

                        A = U

3.5.2. Thế năng biến dạng đàn hồi riêng

        Thế năng biến dạng đàn hồi riêng là thế năng biến dạng đàn hồi trong một đơn vị diện tích:

3.6. Ứng suất cho phép – Hệ số an toàn. Điều kiện bền

3.6.1. Ứng suất cho phép – Hệ số an toàn

Ta gọi trị số ứng suất mà ứng với nó vật liệu được xem là bị phá hủy là ứng suất nguy hiểm ký hiệu là σ₀. Vậy vật liệu làm việc an toàn khi ứng suất xuất hiện chưa vượt quá ứng suất nguy hiểm.

- Đối với vật liệu dẻo:

         σ₀ = σ_ch

- Đối với vật liệu giòn:

         σ₀ = σ_b

Trong thực tế chế tạo, vật liệu thường không đồng chất hoàn toàn, và trong quá trình sử dụng tải trọng tác dụng có thể vượt quá tải trọng thiết kế, điều kiện làm việc của kết cấu hay chi tiết chưa được xem xét đầy đủ, các giả thiết khi tính toán chưa đúng với sự làm việc của kết cấu, do đó khi tính toán thiết kế ta không bao giờ dùng ứng suất nguy hiểm σ₀.

Vì vậy để các chi tiết làm việc an toàn, trong tính toán thiết kế ta phải xác định một giá trị ứng suất cho phép đối với mỗi vật liệu, ký hiệu là [σ] để tính toán. Ứng suất cho phép phải nhỏ hơn ứng suất nguy hiểm và ứng suất lớn nhất phát sinh trong chi tiết không được vượt quá ứng suất cho phép. Ứng suất cho phép được xác định theo công thức:

3.6.2. Điều kiện bền

Thanh chịu kéo nén đúng tâm nội lực chỉ có N_z khác không, tương ứng với ứng suất trên mặt cắt ngang chỉ có ứng suất pháp σ_z. Do đó, muốn đảm bảo sự làm việc an toàn về độ bền khi thanh chịu kéo (nén) đúng tâm, ứng suất trong thanh phải thỏa điều kiện:

3.6.3. Ba bài toán cơ bản

3.7. Bài toán siêu tĩnh

3.7.1. Khái niệm

Hệ siêu tĩnh là hệ mà ta không thể xác định được hết các phản lực liên kết và nội lực trong hệ nếu chỉ nhờ vào các phương trình cân bằng tĩnh học.

3.7.2. Phương pháp giải

Do trong hệ siêu tĩnh số ẩn cần tìm lớn hơ số phương trình cân bằng nên ta phải viết thêm các phương trình bổ sung đó chính là các phương trình biến dạng.

Trình tự giải hệ siêu tĩnh được thực hiện như sau:

Bước 1: Viết phương trình biến dạng, xác định các phản lực liên kết. Xác định phản lực liên kết thừa.

Bước 2: Thực hiện như bài toán tĩnh định với ngoại lực tác dụng vào hệ bao gồm ngoại lực và phản lực