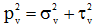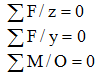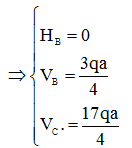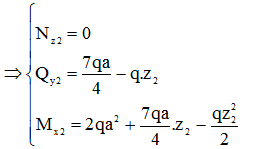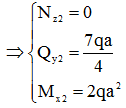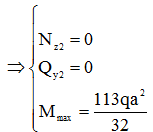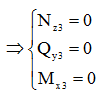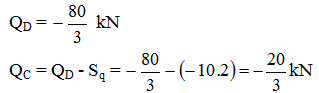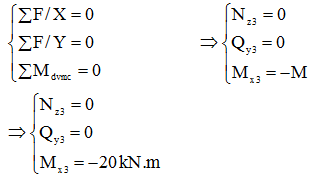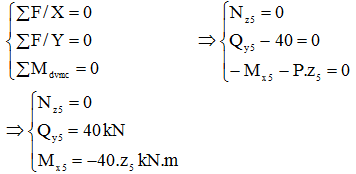CỘNG ĐỒNG XÂY DỰNG ĐẠI HỌC TIỀN GIANG: August 2014

Chương 2:

LÝ THUYẾT NỘI LỰC

2.1. Khái niệm chung

2.1.1. Nội lực

Dưới tác dụng của các tác nhân bên ngoài như tải trọng, sự thay đổi nhiệt độ, … các phân tử của vật thể có khuynh hướng nhích lại gần nhau hơn hoặc tách xa hơn. Khi đó, lực tương tác giữa các phân tử của vật thể phải thay đổi để chống lại khuynh hướng dịch chuyển này. Sự thay đổi của lực tương tác giữa các phân tử trong vật thể được gọi là nội lực.

2.1.2. Phương pháp xác dịnh nội lực

Để xác định nội lực trong vật thể, người ta dùng phương pháp mặt cắt.

* Nội dung phương pháp mặt cắt:

Xét vật thể cân bằng dưới tác dụng của ngoại lực như hình vẽ:

Tưởng tượng một mặt phẳng (α) cắt qua và chia vật thể thành hai phần A và B; hai phần này sẽ tác động lẫn nhau bằng hệ lực phân bố trên diện tích mặt tiếp xúc tuân theo định luật lực và phản lực. Nếu ta tách riêng phần A thì hệ lực tác động từ phần phần B vào nó phải cân bằng với ngoại lực ban đầu như trên hình vẽ:

2.1.3. Ứng suất

Ứng suất tại một điểm trên mặt cắt là độ biến thiên của nội lực trên một đơn vị diện tích của mặt cắt. Công thức tổng quát để xác định ứng suất tại một điểm trên mặt cắt như sau:

Trong đó:

- p_v là ứng suất toàn phần tại điểm khảo sát.

- Δp là vectơ nội lực tác dụng trên diện tích ΔA.

Ứng suất là một đại lượng cơ học đặc trưng cho mức độ chịu đựng của vật liệu tại một điểm. Để đánh giá độ bền của vật liệu ta dựa vào ứng suất, nếu ứng suất vượt quá một giới hạn nào đó thì vật liệu bị phá hoại.

Ứng suất toàn phần p_v có thể được phân thành hai thành phần:

- Thành phần ứng suất pháp σ_v vuông góc với mặt phẳng (α).

- Thành phần ứng suất tiếp τ_v nằm trong mặt phẳng (α).

2.2. Các thành phần ứng lực trên mặt cắt ngang

2.2.1. Trong trường hợp tổng quát

Trên mặt cắt ngang của thanh chịu tác dụng của ngoại lực có 6 thành phần nội lực bao gồm:

- Ba thành phần theo ba trục x, y, z ký hiệu lần lượt là lực dọc N_z, lực cắt Q_y và lực cắt Q_x.

- Ba thành phần quay quanh trục x, y, z ký hiệu lần lượt là mô men uốn M_x, mô men uốn M_y và mô men xoắn M_z.

Sáu thành phần nội lực trên một mặt cắt ngang được xác định từ sáu phương trình cân bằng độc lập của phần vật thể được tách ra trên đó có tác dụng của ngoại lực ban đầu và các thành phần nội lực. Cụ thể là:

Trong đó: m_x(P_i), m_y(P_i), m_z(P_i) lần lượt là mô men của các lực P_i đối với các trục x, y, z.

2.2.2. Trong trường hợp bài toán phẳng

Trong trường hợp bài toán phẳng, giả sử ngoại lực nằm trong mặt phẳng đi qua trục z (yOz) nên chỉ tồn tại các thành phần ứng lực trong mặt phẳng này: N_z, M_x, Q_y.

2.3. Quan hệ giữa nội lực và ứng suất

Các thành phần nội lực có liên quan với các thành phần ứng suất như sau:

- Lực dọc là tổng của các ứng suất pháp.

- Lực cắt là tổng các ứng suất tiếp theo phương đó.

- Mô men uốn là tổng các mô men gây ra bởi các ứng suất đối với trục x hoặc trục y.

- Mô men xoắn là tổng các mô men của các ứng suất tiếp đối với trục z.

Nếu gọi σ_z, τ_zx, τ_zy là các thành phần ứng suất tại điểm Mx,y) trên mặt cắt ngang, ta có các biểu thức:

Trong đó dA là phân tố diện tích bao quanh điểm M(x,y).

2.4. Cách xác định nội lực trong bài toán phẳng

Như chúng ta đã biết, để xác định các thành phần nội lực, người ta sử dụng phương pháp mặt cắt.

2.4.1. Qui ước dấu nội lực

- Lực dọc được xem là dương khi có chiều hướng ra ngoài mặt cắt (nghĩa là gây kéo cho đoạn thanh đang xét).

- Lực cắt được xem là dương khi có khuynh hướng làm quay đoạn thanh đang xét theo chiều kim đồng hồ.

- Mô men uốn được xem là dương khi nó làm căng thớ dưới.

2.4.2. Cách xác định nội lực bài toán phẳng

Để xác định nội lực trong bài toán phẳng, người ta thực hiện như sau:

- Giả thiết chiều các thành phần M_x, N_z, Q_y theo chiều dương qui ước, kết quả giải bài toán nếu thành phần nào mang giá trị âm thì thành phần nội lực đó có chiều ngược lại với chiều giả thiết ban đầu.

- Thiết lập phương trình hình chiếu lên các trục z, y và phương trình cân bằng mômen với trọng tâm O của mặt cắt ngang:

2.5. Biểu đồ nội lực của bài toán phẳng

2.5.1. Biểu đồ nội lực

Thông thường, các nội lực trên mọi mặt cắt ngang của một thanh là không giống nhau. Đường cong biểu diễn sự biến thiên của các nội lực theo vị trí của các mặt cắt gọi là biểu đồ nội lực.

2.5.2. Cách vẽ biểu đồ nội lực

Các bước vẽ biểu đồ nội lực, người ta sử dụng phương pháp mặt cắt biến thiên và được tiến hành theo các bước sau:

- Bước 1: Xác định phản lực tại các liên kết tại các gối liên kết.

- Bước 2: Phân đoạn thanh sao cho biểu thức của các thành phần ứng lực trên từng đoạn là liên tục. (Thông thường là các đoạn có sự thay đổi về ngoại lực tác dụng)

- Bước 3: Viết biểu thức xác định các thành phần ứng lực N_z, Q_y, M_x theo toạ độ mặt cắt ngang bằng phương pháp mặt cắt

- Bước 4: Vẽ biểu đồ cho từng đoạn căn cứ vào phương trình nhận được từ bước 3.

- Bước 5: Kiểm tra biểu đồ nhờ vào các nhận xét mang tính trực quan, tính kinh nghiệm.

2.5.3. Bài tập thí dụ

Cho thanh chịu tác dụng của tải trọng như hình vẽ:

Hãy xác vẽ biểu đồ mô men uốn của dầm.

Giải

Bước 1: Thay thế liên kết gối cố định B bằng 2 thành phần phản lực liên kết và gối di động C bằng 1 thành phần phản lực liên kết như hình vẽ:

Bước 2: Áp dụng điều kiện cân bằng dạng 1:

Ta được:

Kết luận:

- Phản lực liên kết thẳng đứng tại gối B cùng chiều giả thiết ban đầu (chiều hướng lên).

- Phản lực liên kết thẳng đứng tại gối C cùng chiều giả thiết ban đầu (chiều hướng lên).

Bước 3: Chia dầm thành 3 đoạn và sử dụng các mặt cắt 1-1, 2-2, 3-3 cắt qua các đoạn như hình vẽ.

Bước 4: Viết phương trình cân bằng cho các mặt cắt:

- Phương trình cân bằng cho mặt cắt 1-1 (0 ≤ z₁≤ a), khảo sát sự cân bằng của phần hệ bên trái.

Áp dụng điều kiện cân bằng dạng 1:

Ta được:

- Phương trình cân bằng cho mặt cắt 2-2 (0 ≤ z₂≤ 4a), khảo sát sự cân bằng của phần hệ bên trái.

Áp dụng điều kiện cân bằng dạng 1:

Ta được:

+ Tại vị trí z₂ = 0:

+ Tại vị trí z₂ = 4a:

+ Vị trí M_x đạt giá trị cực trị:

- Phương trình cân bằng cho mặt cắt 3-3 (0 ≤ z₂≤ 2a), khảo sát sự cân bằng của phần hệ bên phải.

Áp dụng điều kiện cân bằng dạng 1:

Ta được:

+ Tại vị trí z₃ = 0:

+ Tại vị trí z₃ = 2a:

Bước 5: Biểu đồ nội lực của thanh:

Bước 6: Kiểm tra sự cân bằng tại các nút:

Tại gối B:

2.6. Quan hệ vi phân giữa cường độ tải trọng phân bố, lực cắt và mô men uốn của thanh chịu uốn

Trước hết ta qui ước hệ trục được chọn như sau:

- Đối với biểu đồ lực cắt Q_y - Đối với biểu đồ mô men M_x

2.6.1. Thiết lập công thức quan hệ

Xét dầm chịu tải phân bố q(z) > 0: hướng lên

Tách đoạn thanh có chiều dài dz giới hạn bởi 2 mặt cắt ngang 1-1và 2-2:

Vậy đạo hàm bậc hai của mô men uốn bằng đạo hàm bậc nhất của lực cắt và bằng cường độ tải trọng ngang phân bố.

2.6.2. Ứng dụng

- Nhận dạng các biểu đồ Q_y, M_x khi biết qui luật phân bố của tải trọng q(z): Nếu trên một đoạn thanh biểu thức của q(z) bậc n thì biểu thức lực cắt Q_y bậc (n+1), biểu thức mômen M_x bậc (n+2).

- Tại mặt cắt có Q_y = 0 => M_x đạt cực trị

- Tính các thành phần Q_y, M_x tại mặt cắt bất kỳ khi biết giá trị của chúng tại mặt cắt xác định

- Trên đoạn dầm mà tải trọng phân bố q(z) > 0 (chiều hướng lên) thì biểu đồ mô men uốn là đường cong lõm và ngược lại đoạn dầm mà tải trọng phân bố q(z) < 0 (chiều hướng xuống) thì biểu đồ mô men uốn là đường cong lồi. Nói cách khác, bề lõm của biểu đồ mô men uốn luôn hứng lấy chiều tác dụng của lực phân bố.

2.6.3. Vẽ biểu đồ nội lực theo điểm đặc biệt

Dựa vào mối liên hệ vi phân giữa Q_y, M_x và q(z), ta có thể vẽ nhanh biểu đồ nội lực như sau:

Biết tải trọng phân bố => Nhận xét dạng biểu đồ Q_y, M_y => Xác định số điểm cần thiết để vẽ được biểu đồ.

Trong đó các giá trị Q_A, Q_B, M_A, M_B, cực trị là giá trị các điểm đặc biệt được xác định bởi:

- Quan hệ bước nhảy của biểu đồ

- Phương pháp mặt cắt:

Q_phải = Q_trái+S_q(S_q – Diện tích biểu đồ q)

M_phải = M_trái+S_Q(S_Q – Diện tích biểu đồ Q)

2.6.4. Ví dụ áp dụng

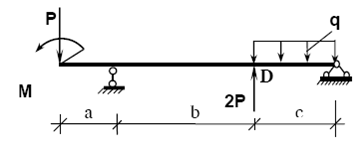
Ví dụ 1: Cho dầm chịu tác dụng của tải trọng như hình vẽ:

Cho biết: a = 1m, b = 4m, c = 2m, P = 20kN, q = 10kN/m, M = 20kN.m

Hãy vẽ biểu đồ nội lực của dầm.

Giải

- Bước 1: Thay thế liên kết gối cố định D bằng 2 thành phần phản lực liên kết và gối di động B bằng 1 thành phần phản lực liên kết như hình vẽ:

Áp dụng điều kiện cân bằng:

Ta được:

Kết luận:

- Phản lực liên kết thẳng đứng tại gối B cùng chiều giả thiết ban đầu (chiều hướng lên).

- Phản lực liên kết thẳng đứng tại gối D ngược chiều giả thiết ban đầu (chiều hướng xuống).

- Bước 2:

+ Đoạn AB: lực phân bố q = 0 nên:

- Biểu đồ lực cắt Q_y là hằng số: Q_A = -20 kN; Q_B = Q_A + S_q = -20 kN

- Biểu đồ mô men uốn là hàm bậc nhất: M_A = 0 và M_B = -20 kN.m

+ Đoạn BC: lực phân bố là hằng số q = -10 kN/m nên:

- Biểu đồ lực cắt Q_y là hàm bậc nhất: Q_B = 20 kN, Q_C = -20 kN

- Biểu đồ mô men uốn là hàm bậc hai: M_B = -20 và M_C = -20 kN.m

- Vì q < 0 nên đường cong bậc 2 lồi

+ Đoạn CD: lực phân bố q = 0 nên:

- Biểu đồ lực cắt Q_y là hằng số: Q_D = 20 kN

- Biểu đồ mô men uốn là hàm bậc nhất: M_D = 20 và M_C = -20 kN.m

- Bước 3: Biểu đồ nội lực

Nhận xét: Dựa vào biểu đồ ta nhận thấy:

- Tại A, B, C, D có lực tập trung thì trên biểu đồ lực cắt có bước nhảy, độ lớn bước nhảy bằng độ lớn của lực tập trung; Khi vẽ từ bên trái sang thì chiều của bước nhảy cùng chiều với lực tập trung.

- Tại D có mô men tập trung thì trên biểu đồ mô men có bước nhảy, độ lớn bước nhảy bằng độ lớn mô men tập trung. Khi vẽ từ bên trái sang thì mô men quay ngược chiều kim đồng hồ bước nhảy đi lên.

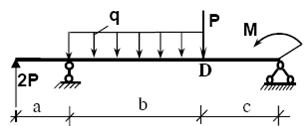
Ví dụ 2: Cho dầm chịu tác dụng của tải trọng phân bố đều, tải trọng tập trung và mô men tập trung như hình:

Cho biết: a = 1m, b = 4m, c = 2m, P = 20kN, q = 10kN/m, M = 20kN.m

Hãy vẽ biểu đồ nội lực của dầm.

Giải

- Bước 1: Thay thế liên kết gối di động B bằng 1 thành phần phản lực liên kết và gối cố định D bằng 2 thành phần phản lực liên kết như hình vẽ:

Áp dụng điều kiện cân bằng:

Ta được:

Kết luận:

- Phản lực liên kết thẳng đứng tại gối B cùng chiều giả thiết ban đầu (chiều hướng lên).

- Phản lực liên kết thẳng đứng tại gối D cùng chiều giả thiết ban đầu (chiều hướng lên).

- Bước 2:

+ Đoạn AB: lực phân bố q = 0 nên:

- Biểu đồ lực cắt Q_y là hằng số:

Q_A = -40 kN

Q_B = Q_A + S_q = -40 kN

- Biểu đồ mô men uốn là hàm bậc nhất:

M_A = 0

M_B = M_A +S_Q= 0 + (-40.1) = -40 kN.m

+ Đoạn BC: lực phân bố q = 0 nên:

- Biểu đồ lực cắt Q_y là hằng số:

- Biểu đồ mô men uốn là hàm bậc nhất:

+ Đoạn CD: lực phân bố đều q = -10 kN/m nên:

- Biểu đồ lực cắt Q_y là hàm số bậc nhất:

- Biểu đồ mô men uốn là hàm bậc hai:

- Bước 3: Biểu đồ nội lực

Nhận xét: Dựa vào biểu đồ ta nhận thấy:

- Tại C có mô men tập trung thì trên biểu đồ mô men có bước nhảy, độ lớn bước nhảy bằng độ lớn mô men tập trung. Khi vẽ từ bên trái sang thì mô men quay cùng chiều kim đồng hồ bước nhảy đi xuống.

2.7. Biểu đồ nội lực dầm tĩnh định nhiều nhịp

2.7.1. Định nghĩa

Dầm tĩnh định nhiều nhịp là hệ tĩnh định gồm tập hợp các dầm, nối với nhau bằng các liên kết khớp.

Dầm tĩnh định nhiều nhịp được chia thành dầm chính và dầm phụ. Dầm chính là dầm khi đứng độc lập vẫn chịu được tải trọng. Dầm phụ là dầm khi đứng độc lập không chịu được tải trọng, phải tựa lên dầm chính mới chịu được tải trọng.

Tải trọng đặt lện dầm chính không ảnh hưởng tới dầm phụ, tải trọng đặt trên dầm phụ sẽ truyền tới dầm chính thông qua phản lực liên kết.

2.7.2. Cách vẽ biểu đồ nội lực

Để vẽ biểu đồ nội lực dầm nhiều nhịp tĩnh định ta thực hiện theo trình tự như sau:

- Bước 1: Phân biệt hệ dầm thành các dầm chính và dầm phụ.

- Bước 2: Vẽ biểu đồ nội lực trên các dầm phụ và xác định phản lực liên kết trên dầm phụ tại các vị trí liên kết với dầm khác.

- Bước 3: Vẽ biểu đồ nội lực trên dầm chính. Chú ý ngoại lực tác dụng lên dầm chính bao gồm ngoại lực tác dụng lên dầm và phản lực liên kết tại các liên kết với dầm phụ.

- Bước 4: Ghép các biểu đồ nội lực của các dầm lại với nhau ta được biểu đồ của dầm nhiều nhịp tĩnh định.
2.7.3. Ví dụ áp dụng

Cho dầm ghép chịu tác dụng của tải trọng tập trung P₁ = 40 kN, P₂ = 50 kN và tải trọng phân bố q = 20 kN/m như hình vẽ:

Hãy vẽ biểu đồ nội lực của dầm.

Giải

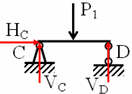
Bước 1: Hệ đã cho có thể tách thành hệ gồm dầm chính ABC và dầm phụ CD như hình vẽ:

Bước 2: Khảo sát dầm phụ CD

Áp dụng điều kiện cân bằng:

Biểu đồ nội lực dầm phụ CD:

Bước 3: Khảo sát dầm chính ABC

Áp dụng điều kiện cân bằng:

Biểu đồ nội lực dầm chính ABC:

Bước 4: Biểu đồ nội lực của dầm ghép ABCD:

2.8. Biểu đồ nội lực khung phẳng

2.8.1. Khái niệm

Khung phẳng là hệ phẳng gồm những thanh nối nhau bằng các liên kết cứng (là liên kết mà góc giữa các thanh tại điểm liên kết không thay đổi khi khung chịu lực).

2.8.2. Qui ước biểu đồ nội lực

- Đối với các đoạn khung nằm ngang, biểu đồ các thành phần ứng lực vẽ như qui ước với thanh thẳng.

- Đối với các đoạn khung thẳng đứng, biểu đồ N, Q vẽ về phía tùy ý và mang dấu. Biểu đồ mômen vẽ về phía thớ căng.

- Để kiểm tra biểu đồ ta cần kiểm tra điều kiện cân bằng các mắt khung: Tại mắt khung, nội lực và ngoại lực thoả mãn điều kiện cân bằng tĩnh học.
2.8.3. Ví dụ áp dụng
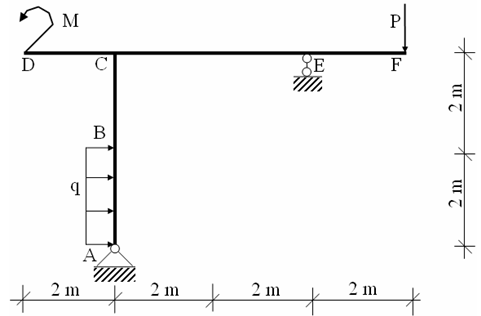
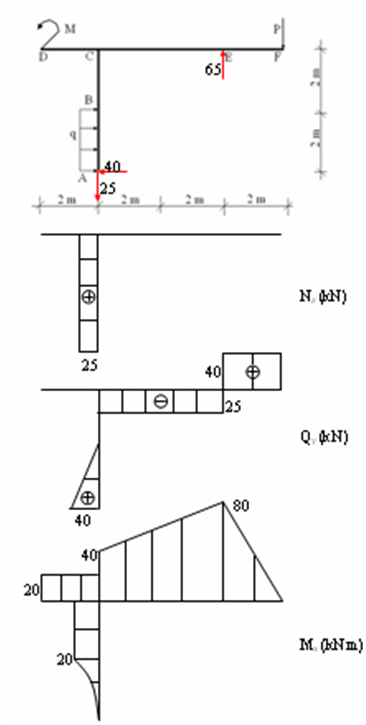
Cho khung phẳng chịu tác dụng của tải trọng tập trung P = 40 kN, tải trọng phân bố q = 20 kN/m và mô men tập trung M = 20 kN.m như hình vẽ: