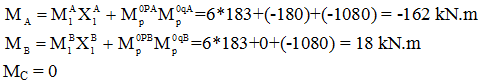TRÌNH TỰ CÁC BƯỚC SỬ DỤNG PHƯƠNG PHÁP LỰC GIẢI BÀI TOÁN SIÊU TĨNH
- Bước 1: Xác định bậc siêu tĩnh
- Bước 2: Chọn hệ cơ bản
- Bước 3: Vẽ biểu đồ mô men uốn thành phần Mi do các lực thành phần Xi gây ra trên hệ cơ bản
- Bước 4: Vẽ biểu đồ mô men uốn Mpo do ngoại lực gây ra trên hệ cơ bản
- Bước 5: Viết phương trình chính tắc:
- Bước 6: Xác định hệ số phương trình chính tắc
- Bước 7: Giải phương trình chính tắc
- Bước 8: Xác định giá trị mô men tại các vị trí đặc biệt
- Bước 9: Vẽ biểu đồ mô men uốn M
- Bước 10: Vẽ biểu đồ lực cắt Q
- Bước 11: Vẽ biểu đồ lực dọc N
BÀI TẬP ÁP DỤNG CÓ LỜI GIẢI
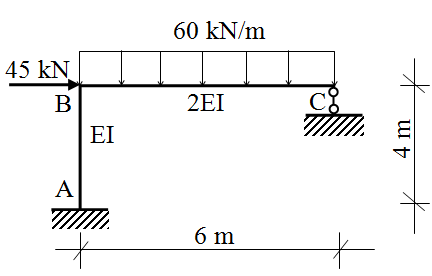
Bài tập 1: Cho khung phẳng chịu tác dụng của tải trọng như
hình vẽ. Hãy vẽ biểu đồ nội lực của khung.
Giải
- Bước 1: Xác định bậc siêu tĩnh:
Hệ khung nên ta có công thức xác định bậc siêu tĩnh là:
n = 3V - K = 3.1 - 2 = 1 (Ở đây số chu vi kín V = 1, số khớp là K = 2)
- Bước 2: Chọn hệ cơ bản
Hệ cơ bản được chọn là hệ bất biến hình tĩnh định. Với khung trên ta chọn như sau:
Tại vị trí gối di động B, ta gỡ bỏ liên kết và thay thế bằng 1 thành phần phản lực X1.
Bước 3: Vẽ biểu đồ mô men uốn thành phần M1 do X1 = 1 gây ra trên hệ cơ bản.
Bước 4: Vẽ biểu đồ mô men uốn Mpo do ngoại lực gây ra trên hệ cơ bản
Ngoại lực tác dụng lên khung gồm tải trọng tập trung và tải trọng phân bố, để đơn giản cho việc tính diện tích và trọng tâm ta áp dụng nguyên lý cộng tác dụng phân tích thành 2 sơ đồ như hình.
- Bước 5: Viết phương trình chính tắc:
- Bước 6: Xác định hệ số phương trình chính tắc
Xác định δ11: Lấy diện tích hình M1 chiếu lên trọng tâm hình M1:
Chú ý: Dấu "-" trong công thức là do biểu đồ của hai hình M1 và Mpo nằm khác phía.
- Bước 7: Giải phương trình chính tắc
- Bước 8: Xác định giá trị mô men tại các vị trí đặc biệt
- Bước 9: Vẽ biểu đồ mô men uốn M
- Bước 10: Vẽ biểu đồ lực cắt Q
Áp dụng công thức:
+ Thanh AB, ta có:
+ Thanh BC, ta có:
Biểu đồ lực cắt Qy:
- Bước 11: Vẽ biểu đồ lực dọc N
Áp dụng công thức:
+ Thanh BC, ta có:
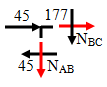
Sử dụng phương pháp tách nút, tách nút B, ta có:
Áp dụng điều kiện cân bằng:
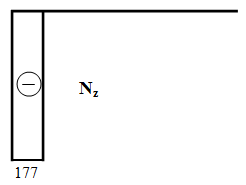
Biểu đồ lực dọc:
